The Exponential Moving Average (or EMA for short) is one of the most commonly used indicators by stock and commodities markets traders. In this guide, we will discuss how to calculate the exponential moving average in a step by step algorithm.
Why is the Exponential Moving Average called “Exponential”
The Exponential Moving Average (EMA) is a weighted moving average. Which means that unlike a simple moving average where the values of the far past have the same weight in the calculation as more recent values, a weighted moving average gives greater significance to more recent values than older one.
This is usually done using a weighting factor. The weighting factor is a factor that is multiplied to each of the values in the calculation. In the EMA calculation, this factor decreases exponentially the further it goes in the past.
How to calculate the Exponential Moving Average
Let us now get into the details of calculating the EMA. One of the obstacles that might make it difficult to understand how the calculation is done is that the EMA is calculated recursively. This means that the value of the EMA of a candle depends on the value of the EMA calculation of the previous candle and so on.
We will discuss the EMA calculation in step by step in order to make things as simple as possible. Let us start by displaying the general formula of the EMA calculation.
EMA (Last time period) = Value(Now) x Smoothing Factor + (1 – Smoothing factor) x EMA (Previous period)
EMA (First Time Period) = Value (First time period)
Smoothing Factor = 2 / (Number of time periods + 1)
When calculating the EMA, you will need to decide how many time periods you will use. The more time periods you use, the better the signals that are emitted from the indicator are. For example, if you are using the daily chart, and you decide to calculate the 21 day EMA, then the number of time periods in the calculation is 21.
Now let us go through the calculation algorithm step by step in order to explain how the EMA is calculated.
Calculating the smoothing factor
Remember when we mentioned that the EMA uses a weighting factor. This is also called the Smoothing Factor in this formula. If you would like to calculate the value of the factor for a 21 day EMA, then the calculation would be as follows:
Smoothing Factor = 2 / (21 + 1) = 0.0909090909090909..
Notice that the number will always be less than 1. Please also note that this formula is an approximation of the value of the EMA. If you would like to calculate the factor’s value to the 100th decimal point as a scientist, then yo will need to perform a much more complicated calculation which you could find in scientific textbooks. But do not worry, as this approximation formula is used in most trading systems.
Another thing to point out that as a result of the recursive nature of the formula, and the multiplying of the (1 – smoothing factor) with the previous EMA value, the weight of the previous EMA value decreases the more we go into the past. This can be visualized in the next chart.
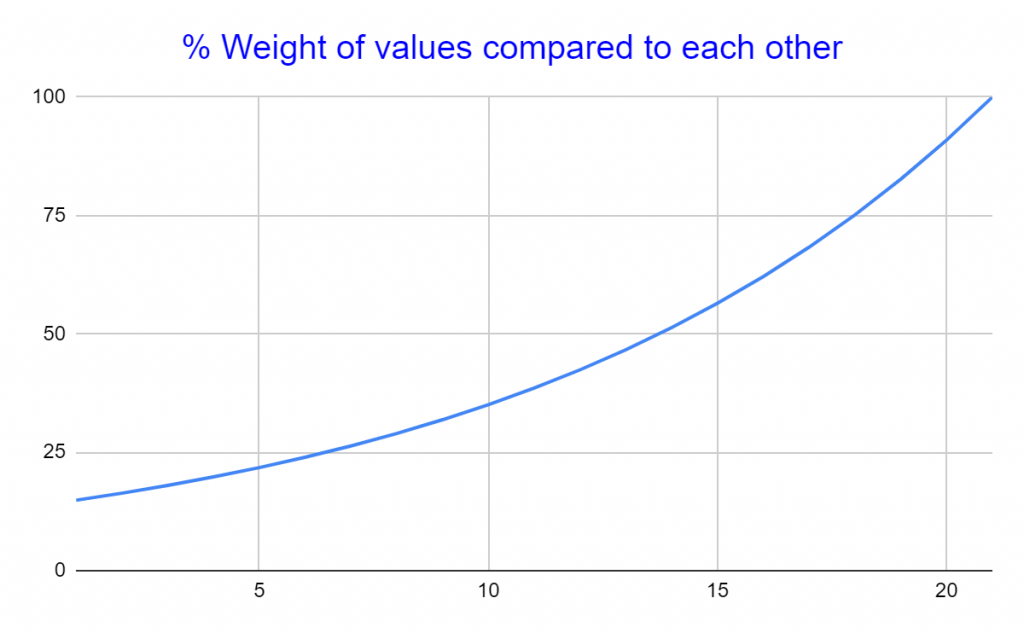
Click to enlarge
Calculating the first intermediate EMA
The first intermediate EMA value is simply the price value of the first day in the EMA calculation. For example, if your data looks as follows and you would like to calculate the 21 day EMA:
- Day 1 (10th Oct): $200
- Day 2 (11th Oct): $202
- …..
- Day 21 (31st Oct): $212
Then when calculating the 21 day EMA for the 31st of October, the first intermediate EMA is the value of day 1, which is $200.
Please note that you could also use the 21 day EMA of Day 1 if you already have it as it can provide a more accurate calculation. More on that later.
Calculating the final EMA value
Now that we have the starting ingredients for calculating the EMA, we can start to calculate the final EMA value. As we mentioned previously, the EMA value is recursively calculated. Which means the current value depends on the previous value, and the previous value depends on the one before it, and so on. Take a look at the following diagram.
As you can see, each EMA calculation depends on the subsequent one. For simplicity purposes, let us calculate the 3 day EMA on Oct 22nd of the following data:
- 19th Oct: $10
- 20th Oct: $11
- 21st Oct: $12
- 22nd Oct: $13
Using our formula:
Smoothing Factor (SF) = 2 / (3+1) = 0.5
EMA(1) = Price(1) = 10
EMA(2) = 0.5 * 11 + (1 – 0.5) * 10 = 10.5
EMA(3) = 0.5 * 12 + (1 – 0.5) * 10.5 = 11.25
It is important to highlight that in our examples, all EMAs calculated except for the last ones are intermediate EMAs. In the example above, the EMA(2) is only an intermediate EMA for that date that is used to calculate the EMA of day 3.
If you need to calculate a more accurate 3-day EMA of day 2 (the 20th of October), then you will need to go back 3 days in the past! (from Oct 17 to Oct 19).
So you might ask, if the calculation is recursive, and we can always go back in the past, does this mean that our calculation is wrong? Well no!
For example, if you would like to calculate the 14 day EMA of a specific chart, you can either use the price value of day 1 to start your calculations, or you can use the 14 day EMA value of day 1 if you already have it.
Using the actual EMA value as a start of your calculations will yield more accurate results. However, it is often not practical as you can have years or decades of price data, and it is not always possible to calculate the EMA values since the start of time, just to have the 14, 21 or X day EMA of a specific date. This is why we use the 1st price value in our calculations as a compromise.
This is why the first few EMA values are sometimes called “spin-up” values, as they help to start the EMA calculations, but may not be so accurate themselves.
Calculating the Exponential Moving Average (EMA) in Java
You know that we wouldn’t end this tutorial without providing code samples in Java 😉 . All we have to do is implement our algorithm that we discussed above in order to calculate the EMA. Our data will be structured in a class called “Candlestick”. Each candlestick holds the closing price of the commodity for that date.
So given an array of candlesticks, we can recursively loop through the array in order to calculate the EMA of each day. Our calculate method takes as input the Candlesticks and the number of time periods n in order to calculate the EMA.
Note that we will assume that the first candlestick represents the “beginning of time candle”. Therefore, our results will have the same number of values as candlesticks and we will produce final EMA values from the first candlestick value.
package com.example.demo.indicators;
import com.binance.api.client.domain.market.Candlestick;
/**
* EMA calculation example
* By: nullbeans.com
*/
public class EmaIndicator {
/**
* Calculates the Exponential moving average (EMA) of the given data
* @param candlesticks
* @param n : number of time periods to use in calculating the smoothing factor of the EMA
* @return an array of EMA values
*/
public static double[] calculateEmaValues(Candlestick[] candlesticks, double n){
double[] results = new double[candlesticks.length];
calculateEmasHelper(candlesticks, n, candlesticks.length-1, results);
return results;
}
public static double calculateEmasHelper(Candlestick[] candlesticks, double n, int i, double[] results){
if(i == 0){
results[0] = Double.parseDouble(candlesticks[0].getClose());
return results[0];
}else {
double close = Double.parseDouble(candlesticks[i].getClose());
double factor = ( 2.0 / (n +1) );
double ema = close * factor + (1 - factor) * calculateEmasHelper(candlesticks, n, i-1, results) ;
results[i] = ema;
return ema;
}
}
}
Important notes and summary
In this guide we discussed how to calculate the Exponential moving average in a step by step manner. We also discussed how the first intermediate EMA value can be calculated. Finally, we discussed how to calculate the EMA using the Java programming language.
Before we go, we wanted to highlight a few important things:
- You can initialize the first intermediate EMA value using different methods than ones highlighted in this tutorial. For example, by calculating an x-candle SMA for that time period.
- The first few EMA values are usually not reliable if you start your calculations from the actual price of the commodity. That is why it is sometimes better to use a longer interval EMA than a shorter one.
- You can base your EMA calculations on the closing price values. This is called the closing EMA. However, you could also use opening price values, highs, lows, etc.. if you prefer.

Leave a Reply
You must be logged in to post a comment.